
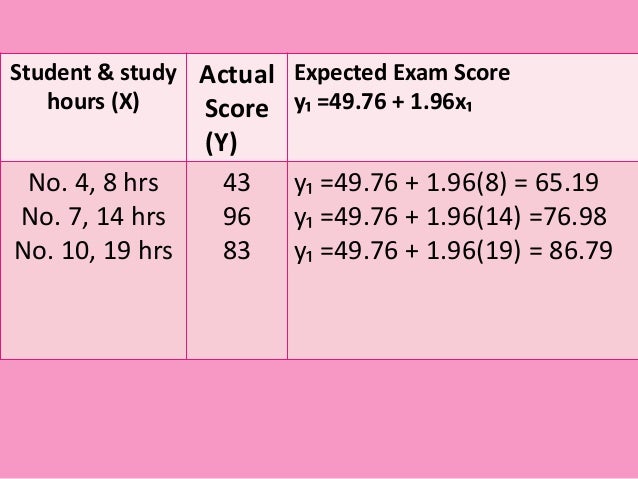
But it does not go far enough, because correlation measures only linear dependence between u and x.

Assuming that u and x are uncorrelated goes a long way toward defining the sense in which u and x should be unrelated in equation (2.1). If u and x are uncorrelated, then, as random variables, they are not linearly related. A natural measure of the association between two random variables is the correlation coefficient. We now turn to the crucial assumption regarding how u and x are related. Importantly, assume (2.3) says nothing about the relationship between u and x but simply makes a statement about the distribution of the unobservables in the population. As long as the intercept β 0 is included in the equation, nothing is lost by assuming that the average value of u in the population is zero. Because u and x are random variables, we need a concept grounded in probability.īefore we state the key assumption about how x and u are related, there is one assumption about u that we can always make. Without such a restriction, we will not be able to estimate the ceteris paribus effect, β 1. We are only able to get reliable estimators of β 0 and β 1 from a random sample of data when we make an assumption restricting how the unobservable u is related to the explanatory variable x. How can we hope to learn in general about the ceteris paribus effect of x on y, holding other factors fixed, when we are ignoring all those other factors? Is this the end of the causality issue? Unfortunately, no. We just saw in equation (2.2) that ( β 1 does measure the effect of x on y, holding all other factors (in u) fixed. The most difficult issue to address is whether model (2.1) really allows us to draw ceteris paribus conclusions about how x affects y. This is unrealistic for many economic applications.For example, in the wage-education example, we might want to allow for increasing returns: the next year of education has a larger effect on wages than did the previous year. The linearity of (2.1) implies that one-unit change in x has the same effect on y,regardless of the initial value of x. Thus, the change in y is simply β 1 multiply bu the change in x.This means that β 1 is the slope parameter in the relationship between y and x holding the other factors in u fixed it is of primary interest in applied economics.The intercept parameter β 0 also has its use ,although it is rarely central to analysis. If the other factors in u are held fixed, so that the change in u is zero,d(u)=0(d=delta),then x has a linear effect on y: A simple regression analysis effectively treats all factors affecting y other than x as being unobserved. The variable u, called the error term or disturbance in the relationship,represents factors other than x that affect y. x is called the independent variable, the explanatory variable, the control variable,the predictor variable,the regressor.(The term covariate is also used for x). When related to this equation the variable y and x have several different names used interchangeably,as follows.y is called the dependent variable, the explained variable, the response variable, the predicted variable, or the regressand. It is also called the two-variable linear regression model or bivariate linear regression model because it relates the two variables x and y.
This equation defines the simple linear regression model. We can resolve these ambiguities by writing down an equation relating y to x. In writing down a model that will “explain y in terms of x”, we must confront three issues.First, since there is never an exact relationship between two variables, how do we allow for other factors to affect y? Second, what is the functional relationship between y and x? And, third, how can we be sure we are capturing a ceteris paribus relationship between y and x(if that is a desired goal)? Much of applied econometric analysis begins with the following premise:y and x are two variables,representing some population, and we are interested in “explaining y in terms of x”, or in “studying how y varies with change of x”.
#Economics simple linear regression equation how to
Learning how to interpret the simple regression model is good practice for studying multiple regression. Nevertheless, it is sometimes appropriate as an empirical tool.

The simple regression model can be used to study the relationship between two variables.For reasons we will see,the simple regression model has limitations as a general tool for empirical analysis.


 0 kommentar(er)
0 kommentar(er)
